Bất đẳng thức Cauchy
Trong toán học, bất đẳng thức Cauchy, bất đẳng so sánh giữa trung bình cộng và trung bình nhân của n số thực không âmđược phát biểu như sau:
- Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng, và trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.
- Với 2 số:
-
- Đẳng thức xảy ra khi và chỉ khi

- Đẳng thức xảy ra khi và chỉ khi
- Với n số:
-
-
-
- Đẳng thức xảy ra khi và chỉ khi

-
-
Tổng quát
Trung bình có hệ số
Cho n số x1, x2,..., xn ≥ 0
và các hệ số α1, α2,..., αn > 0.
Đặt 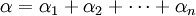 .
.
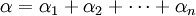 .
.
Bất đẳng thức trung bình cộng và trung bình nhân cũng đúng nếu hai giá trị trung bình có hệ số, như sau:
Dấu " = " xảy ra khi và chỉ khi 

Với các loại trung bình khác
Đẳng thức khi và chỉ khi 

Ví dụ ứng dụng
Cho hàm số sau:
Với x, y và z là các số thực dương. Giả sử rằng ta phải tìm giá trị nhỏ nhất của hàm số đã cho. Biến đổi và áp dụng bất đẳng thức Cauchy ta có:
Vậy ta có giá trị nhỏ nhất của:
Chứng minh bằng quy nạp
Đặt:
bất đẳng thức tương đương với
x1,...,xn là các số thực không âm, ta có:
x1,...,xn là các số thực không âm, ta có:
dấu bằng xảy ra nếu μ = xi với mọi i = 1,...,n.
Chứng minh dưới đây áp dụng phương pháp quy nạp toán học.
Cơ sở: với n = 1 bất đẳng thức đúng.
Giả thiết quy nạp: giả sử rằng bất đẳng thức đúng với n (n lớn hơn hoặc bằng 1).
Quy nạp: xétn + 1 số thực không âm. Ta có:
Nếu tất cả các số đều bằng μ, thì ta có đẳng thức và đã được chứng minh. Ngược lại, ta sẽ tìm được ít nhất một số nhỏ hơn μvà một số lớn hơn μ, không mất tính tổng quát, xem rằng: xn > μ và xn+1 < μ. Ta có:
Xét n số sau:
 với
với 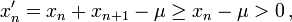
cũng là số không âm. Từ đó:
μ cũng là trung bình cộng của  và theo giả thuyết quy nạp ta có
và theo giả thuyết quy nạp ta có
 và theo giả thuyết quy nạp ta có
và theo giả thuyết quy nạp ta có
Mặt khác từ (*) ta có
hay là
hiển nhiên μ > 0. Nếu có ít nhất một trong x1,...,xn−1 bằng không, ta dễ thấy bất đẳng thức đúng và dấu bằng không xảy ra. Ngược lại, từ (**) và (***) ta có:
bất đẳng thức được chứng minh.
Chứng minh của Pólya
George Pólya đưa ra một chứng minh cho bất đẳng thức như sau. Gọi f(x) = ex−1 − x, có đạo hàm f'(x) = ex−1 − 1. Ta thấyf'(1) = 0 và từ đó f có giá trị nhỏ nhất tại f(1) = 0. Từ đó x ≤ ex−1 đối với mọi số thực x.
Xét một dãy các số thực không âm 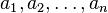 với trung bình cộng μ. Áp dụng bất đẳng thức ở trên ta có:
với trung bình cộng μ. Áp dụng bất đẳng thức ở trên ta có:
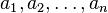 với trung bình cộng μ. Áp dụng bất đẳng thức ở trên ta có:
với trung bình cộng μ. Áp dụng bất đẳng thức ở trên ta có:
Nhưng số mũ có thể rút gọn thành:
Trở lại (1),
và tương đương với:[1]
Chứng minh của Cauchy
Các trường hợp tất cả các giá trị bằng nhau
Nếu tất cả các giá trị bằng nhau:
tức tổng chúng là nx1, do đó giá trị trung bình cộng là x1; và tích các số dưới căn bậc hai là x1n, do dó giá trị trung bình nhân lúc này là x1; vì vậy, vế một và vế 2 bằng nhau, điều phải chứng minh.
Các trường hợp các giá trị không bằng nhau
Nếu tất cả các giá trị bằng nhau không bằng nhau, thì giá trị trung bình cộng lớn hơn giá trị trung bình nhân. Rõ ràng, điều này chỉ có thể xả ra khi n> 1. Trường hợp này khá phức tạp và được chia ra nhiều trường hợp để chứng minh.
Trường hợp n = 2
Nếu n= 2, tức có hai giá trị x1 và x2, và từ giả thiết ở trên, ta có:
điều phải chứng minh.
Trường hợp n = 2k
Xem xét các trường hợp n= 2 k, với k là một số nguyên dương. Chúng tôi tiến hành bằng quy nạp toán học.
Trong trường hợp cơ bản,k = 1, tức n = 2, bất đẳng thức đã được chứng minh ở trên.
Khi, có một giá trị k> 1 bất kỳ, giả sử rằng bất đẳng thức đúng với n = 2k−1, và cần chứng minh rằng nó vẫn đúng khi n = 2k. Để làm như vậy, các bước được thực hiện như sau:
với bất đẳng thức đầu tiên, hai bên đều bằng nhau chỉ khi cả hai điều sau đây là đúng:
(Trong trường hợp này, trung bình số học thứ nhất và trung bình nhân thứ 1 bằngx1, và tương tự với trung bình số học thứ hai và trung bình nhân thứ 2); và trong bất đẳng thức thứ hai, Hai bên chỉ bằng nhau nếu hai giá trị trung bình bằng nhau. Vì không phải tất cả 2 k đều bằng nhau, không thể cho cả hai bất đẳng thức được đẳng, vì vậy chúng ta biết rằng:
(điều phải chứng minh).
Trường hợp n < 2k
Nếu n không phải là một hàm mũ tự nhiên cơ số 2, thì nó chắc chắn là nhỏ hơn một số nào đó theo hàm mũ tự nhiên cơ số 2, vì chuỗi 2, 4, 8,..., 2k,... không bị chặn trên. Do đó, mà không mất tính tổng quát, với m giá trị tuân theo hàm mũ tự nhiên cơ số 2 lớn hơn n.
Vì vậy, nếu ta có n số, thì ta có thể biểu diễn giá trị trung bình cộng α, và được mở rộng như sau:
Chúng tôi sau đó có:
như vậy
điều phải chứng minh.
Bài tập vận dụng:
II. BÀI TẬP ÁP DỤNG
VẤN ĐỀ: Chứng minh BĐT bằng cách sử dụng BĐT Cô–si
Bài 1. Cho a, b, c ³ 0. Chứng minh các bất đẳng thức sau:

Bài 2. Cho a, b, c ³ 0. Chứng minh các bất đẳng thức sau:

Bài 3. Cho a, b, c > 0. Chứng minh các bất đẳng thức sau:

Bài 4. Cho a, b > 0. Chứng minh  . Áp dụng chứng minh các BĐT sau:
. Áp dụng chứng minh các BĐT sau:
 . Áp dụng chứng minh các BĐT sau:
. Áp dụng chứng minh các BĐT sau:

c. Cho a, b, c > 0 thoả 

Bài 5. Cho a, b, c > 0. Chứng minh  . Áp dụng chứng minh các BĐT sau:
. Áp dụng chứng minh các BĐT sau:
 . Áp dụng chứng minh các BĐT sau:
. Áp dụng chứng minh các BĐT sau: .
.
b. Cho x, y, z > 0 thoả x + y + z = 1. Tìm GTLN của biểu thức: 

III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho a, b, c ³ 0. Chứng minh các bất đẳng thức sau:



Bài 2. Cho a, b, c > 0. Chứng minh các bất đẳng thức sau: 9(a3 + b3 + c3) ³ (a + b + c)3
HD: Áp dụng bài 3b) ta có: 9(a3 + b3 + c3) ³ 3(a + b + c)(a2 + b2 + c2)
Từ đó ta được: 3(a2 + b2 + c2) ³ (a + b + c)2 Þ đpcm.
Bài 3. Cho a, b > 0. Chứng minh  (1). Áp dụng chứng minh các BĐT sau:
(1). Áp dụng chứng minh các BĐT sau:
 (1). Áp dụng chứng minh các BĐT sau:
(1). Áp dụng chứng minh các BĐT sau:
b. Cho x, y, z > 0 thoả x + 2y + 4z = 12. Chứng minh: 

c. Cho a, b, c là độ dài ba cạnh của một tam giác, p là nửa chu vi. Chứng minh rằng:

HD a. Theo (1): 

Cùng với các BĐT tương tự, cộng vế theo vế ta được đpcm.
b. Áp dụng câu d) với a = x, b = 2y, c = 4z thì a + b + c = 12 Þ đpcm.
c. Nhận xét: (p –a) + (p – b) = 2p – (a + b) = c.

![\frac{x_1 + x_2 + ... + x_n}{n} \geq \sqrt[n]{x_1.x_2. ... .x_n}](http://upload.wikimedia.org/math/0/f/7/0f7b4ad63905b541aa31244dd6474466.png)

![\frac{\alpha_1 x_1 + \alpha_2 x_2 + \cdots + \alpha_n x_n}{\alpha} \geq \sqrt[\alpha]{x_1^{\alpha_1} x_2^{\alpha_2} \cdots x_n^{\alpha_n}}](http://upload.wikimedia.org/math/d/7/2/d7285ff8e6f3ba98e1dc0934631c1c20.png)
![\frac {n} {\frac{1}{x_1} + \frac{1}{x_2} + ... + \frac{1}{x_n}} \leq \sqrt[n]{x_1x_2...x_n} \leq \frac{x_1+x_2+...+x_n}{n}](http://upload.wikimedia.org/math/6/c/8/6c8769d5aba505f331d67f99ed739a94.png)
![f(x,y,z) = \frac{x}{y} + \sqrt{\frac{y}{z}} + \sqrt[3]{\frac{z}{x}}](http://upload.wikimedia.org/math/8/8/e/88e5021c1ad6a1281047db168dbc2685.png)

![= 6 \cdot \frac{ \frac{x}{y} + \frac{1}{2} \sqrt{\frac{y}{z}} + \frac{1}{2} \sqrt{\frac{y}{z}} + \frac{1}{3} \sqrt[3]{\frac{z}{x}} + \frac{1}{3} \sqrt[3]{\frac{z}{x}} + \frac{1}{3} \sqrt[3]{\frac{z}{x}} }{6}](http://upload.wikimedia.org/math/d/9/6/d96656a0441b7cb921e81a5c5f353e21.png)
![\ge 6 \cdot \sqrt[6]{ \frac{x}{y} \cdot \frac{1}{2} \sqrt{\frac{y}{z}} \cdot \frac{1}{2} \sqrt{\frac{y}{z}} \cdot \frac{1}{3} \sqrt[3]{\frac{z}{x}} \cdot \frac{1}{3} \sqrt[3]{\frac{z}{x}} \cdot \frac{1}{3} \sqrt[3]{\frac{z}{x}} }](http://upload.wikimedia.org/math/e/3/5/e353352b6a83dfeceb11c227b7e0bf9c.png)
![= 6 \cdot \sqrt[6]{ \frac{1}{2 \cdot 2 \cdot 3 \cdot 3 \cdot 3} \frac{x}{y} \frac{y}{z} \frac{z}{x} }](http://upload.wikimedia.org/math/1/a/8/1a81489fe124459677e06fc1f69afb5d.png)

![f(x,y,z) \mbox{là} 2^{2/3} \cdot 3^{1/2} \quad \mbox{khi} \quad \frac{x}{y} = \frac{1}{2} \sqrt{\frac{y}{z}} = \frac{1}{3} \sqrt[3]{\frac{z}{x}}.](http://upload.wikimedia.org/math/b/d/4/bd4debba7fb4205cd6abd50edac93ef8.png)


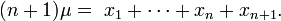

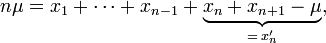





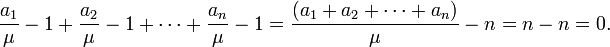

![a_1 a_2 \cdots a_n \le \mu^n \implies \sqrt[n]{a_1 a_2 \cdots a_n} \le \mu.](http://upload.wikimedia.org/math/b/f/3/bf35b9d6c2bc10eaa63e9c52b9bd767c.png)
![\begin{align}
x_1 & \ne x_2 \\[3pt]
x_1 - x_2 & \ne 0 \\[3pt]
\left( x_1 - x_2 \right) ^2 & > 0 \\[3pt]
x_1^2 - 2 x_1 x_2 + x_2^2 & > 0 \\[3pt]
x_1^2 + 2 x_1 x_2 + x_2^2 & > 4 x_1 x_2 \\[3pt]
\left( x_1 + x_2 \right) ^2& > 4 x_1 x_2 \\[3pt]
\Bigl( \frac{x_1 + x_2}{2} \Bigr)^2 & > x_1 x_2 \\[3pt]
\frac{x_1 + x_2}{2} & > \sqrt{x_1 x_2}
\end{align}](http://upload.wikimedia.org/math/9/4/1/9410e577cf28a28c506d0e30926da6c2.png)
![\begin{align}
\frac{x_1 + x_2 + \cdots + x_{2^k}}{2^k} & {} =\frac{\frac{x_1 + x_2 + \cdots + x_{2^{k-1}}}{2^{k-1}} + \frac{x_{2^{k-1} + 1} + x_{2^{k-1} + 2} + \cdots + x_{2^k}}{2^{k-1}}}{2} \\[7pt]
& \ge \frac{\sqrt[2^{k-1}]{x_1 x_2 \cdots x_{2^{k-1}}} + \sqrt[2^{k-1}]{x_{2^{k-1} + 1} x_{2^{k-1} + 2} \cdots x_{2^k}}}{2} \\[7pt]
& \ge \sqrt{\sqrt[2^{k-1}]{x_1 x_2 \cdots x_{2^{k-1}}} \sqrt[2^{k-1}]{x_{2^{k-1} + 1} x_{2^{k-1} + 2} \cdots x_{2^k}}} \\[7pt]
& = \sqrt[2^k]{x_1 x_2 \cdots x_{2^k}}
\end{align}](http://upload.wikimedia.org/math/d/b/a/dba1815ae5a676631bbe679237515771.png)

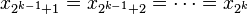
![\frac{x_1 + x_2 + \cdots + x_{2^k}}{2^k} > \sqrt[2^k]{x_1 x_2 \cdots x_{2^k}}](http://upload.wikimedia.org/math/5/b/e/5be511a9650db2e6ef025a7493d1d91d.png)

![\begin{align}
\alpha & = \frac{x_1 + x_2 + \cdots + x_n}{n} \\[6pt]
& = \frac{\frac{m}{n} \left( x_1 + x_2 + \cdots + x_n \right)}{m} \\[6pt]
& = \frac{x_1 + x_2 + \cdots + x_n + \frac{m-n}{n} \left( x_1 + x_2 + \cdots + x_n \right)}{m} \\[6pt]
& = \frac{x_1 + x_2 + \cdots + x_n + \left( m-n \right) \alpha}{m} \\[6pt]
& = \frac{x_1 + x_2 + \cdots + x_n + x_{n+1} + \cdots + x_m}{m} \\[6pt]
& > \sqrt[m]{x_1 x_2 \cdots x_n x_{n+1} \cdots x_m} \\[6pt]
& = \sqrt[m]{x_1 x_2 \cdots x_n \alpha^{m-n}}\,,
\end{align}](http://upload.wikimedia.org/math/b/c/2/bc2e5e9141d6a002a95c74952b8f14ef.png)
![\begin{align}
\alpha^m & > x_1 x_2 \cdots x_n \alpha^{m-n} \\[5pt]
\alpha^n & > x_1 x_2 \cdots x_n \\[5pt]
\alpha & > \sqrt[n]{x_1 x_2 \cdots x_n}
\end{align}](http://upload.wikimedia.org/math/1/0/a/10ac985e1d4f8088bd50527bb6471adf.png)
0 Nhận xét :
Đăng nhận xét