Bất đẳng thức Bunyakovsky

Bách khoa toàn thư mở Wikipedia

Bất đẳng thức Bunhia hay còn gọi là Bất đẳng thức Bunyakovsky được Victor Yakovlevich Bunyakovsky đưa ra để chứng minh các bất đẳng thức trong toán học.

Một số dạng cơ bản

Bất đẳng thức Bunyakovsky dạng thông thường

• (a² + b²)(c² + d²) ≥ (ac + bd)²
• Bất đẳng thức này dễ dàng chứng minh bằng cách khai triển, rút gọn và biến đổi thành: (ad - bc)² ≥ 0
• Dấu " = " xảy ra khi 
  
  

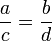
Bất đẳng thức Bunyakovsky cho 2 bộ số

• Với hai bộ số  và  ta có :

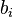• Dấu "=" xảy ra khi và chỉ khi  với quy ước nếu một số  nào đó (i = 1, 2, 3,..., n) bằng 0 thì tương ứng bằng 0.

Bài tập ứng dụng:

Bài 1. Cho a, b, c Î R. Chứng minh các bất đẳng thức sau:

Bài 2. Cho a, b ³ 0 . Chứng minh bất đẳng thức: a³ + b³ ³ a²b + b²a = ab(a + b) (1). Áp dụng chứng minh các bất đảng thức sau:

Bài 3. Cho ba số không âm a, b, c và a + b +c ≤ 3. Chứng minh :

Bài 4. Cho x, y > 0. Chứng minh rằng: 

Bài 5. Tìm giá trị lớn nhất của hàm số 

III. BÀI TẬP ĐỀ NGHỊ

Bài 1.

a. Cho a, b > 0. Chứng minh: 

Hd : sử dụng BĐT Côsi cho hai số dương a, b và 1 + ab

b. Cho x ≥ 1, y ≥ 1. Chứng minh: 

c. Cho a, b, c Î R, thỏa mãn a + b + c = 1. Chứng minh: 

Bài 2. Cho a, b, c > 0. Chứng minh  (1). Áp dụng chứng minh các BĐT sau:

a. Cho a, b, c > 0 thoả a + b + c £ 1. Tìm GTNN của biểu thức:

     .

b. Cho a, b, c > 0 thoả a + b + c = 1. Chứng minh: 

Bài 3. Cho x, y, z là ba số dương và x + y + z £ 1. Chứng minh rằng:

            

HD: Áp dụng BĐT (B), ta có:

Chúc Các bạn học tốt!