Đề cương ôn tập hình học lớp 9 học kỳ 2 (hướng giải dẫn chi tiết)

Bài 1 :

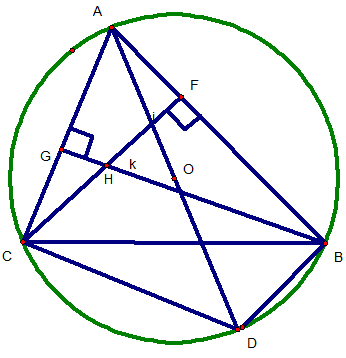
Cho tam giác ABC có 3 góc nhọn. đường tròn (O) có đường kính BC cắt AB, AC lần lượt tại E và D. BD và CE cắt nhau tại H.

1. Chứng minh : H là trực tân của tam giác ABC.
2. Chứng minh : tứ giác AEHD nội tiếp được, xác định tâm I của đường tròn ngoại tiếp.
3. Gọi F là giao điểm của AH và BC. Chứng minh : tứ giác BEHF nội tiếp và AE.AB = AH.AF = AD.AC
4. Chứng minh : 
5. Chứng minh : IE là tiếp tuyến của đường tròn (O).

GIẢI.

1. H là trực tân của tam giác ABC :

Ta có :  (gnt chắn ½ đường tròn )

=> BD 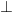  CD tại D.

Cmtt 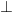: BE   BE

Xét tam giác ABC có :

BD 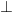  CD (cmt) => BD đường cao thứ nhất.

BE 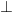  BE (cmt) => CE đường cao thứ hai.

hai đường cao BD và CE cắt nhau tại H (gt)

= > H là trực tâm của tam giác ABC

2. tứ giác AEHD nội tiếp :

xét tứ giác AEHD , ta có :

  (cmt)

  (cmt)

=>

=> tứ giác AEHD nội tiếp đường tròn (I) (tổng 2 góc đối bằng 180⁰ )

Mà :   (cmt)

=> AH là đường kính (I)

=> I là trung điểm của AH.

3. AE.AB = AH.AF = AD.AC

Ta có : AH 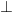  BC tại F (H là trực tâm của tam giác ABC)

Xét Δ FAB và Δ EAH, ta có :

Góc A chung.

=> Δ FAB đồng dạng Δ EAH (g – g)

=> 

=> AE.AB = AH.AF

Cmtt, ta được : AH.AF = AD.AC

=> AE.AB = AH.AF = AD.AC

4.

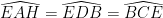
Xét đường tròn (I), ta có :

 (gnt cùng chắn cung AH)

Hay .

Xét đường tròn (O), ta có :

 (gnt cùng chắn cung BE)

=> 

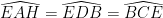
5.IE là tiếp tuyến của đường tròn (O).

Ta có :   (1)()

Xét Δ AEI, ta có : IA = IE (bán kính)

=> Δ AEI cân tại I

=>  (2)

Cmtt, ta được :  (3)

Từ (1), (2) và (3), ta được :

Mà : :

=> 

Hay : 

=> IE 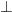 EO tại E

Mà : E thuộc (O)

Vậy :  IE là tiếp tuyến của đường tròn (O).

BÀI 2 :

Cho tam giác ABC nội tiếp đường tròn (O) đường kính AD. H là trực tâm tam giác ABC. Kẻ đường hính OI vuông góc BC tại I. Chứng minh :

1. BHCD là hình bình hành.
2. I, H, D thẳng hàng.
3. AH = 2OI

 GIẢI

BHCD là hình bình hành :

hinh hoc lop 9 – goc trong duong tron

 (góc nội tiếp chắn ½ (O))

=> CD  AC

Mà : BH  AC (H là trực tâm)

=> CD // BH (cùng vuông góc AC)

Cmtt, ta được : BD // CH

Xét tứ giác BHCD , ta có :

BHCD là hình bình hành

CD // BH (cmt)

BD // CH (cmt)

tứ giác BHCD là hình bình hành.

b)I, H, D thẳng hàng.

đường kính OI  BC tại I

=> IB = IC

Mà : hai đường chéo HD và BC của hình bình hành BHCD cắt nhau tại trung điểm mỗi đường.

=> IH = ID

Hay I, H, D thẳng hàng.

3. AH = 2OI

Xét Δ ABC có H là trực tâm

=> AH  BC

Mà : OI  BC

=> OI // AH

Xét Δ AHD, ta có :

OA = OD (AD là  đường kính của (O))

OI // AH (cmt)

=> OI là đường trung bình trong Δ AHD

=> AH = 2OI

Bài tập rèn luyện kỹ năng :

Bài 1 :

Cho đường tròn (O; R) đường kính BC. Lấy điểm A trên (O) sao cho AB = R. vẽ đường cao AH của tam giác ABC. Đường tròn (I) đường kính AH cắt AB và AC lần lượt tại D và E, cắt (O) tại F.

1. Chứng minh : ADHE là hình chữ nhật.
2. Chứng minh : tứ giác BDEC nội tiếp.
3. Chứng minh : OA vuông góc DE.
4. Tính diện tích tứ giác BDEC theo R.

Bài 2 :

Từ điểm A ở ngoài đường tròn (O) vẽ hai tiếp tuyến AB, AC và cát tuyến AEF với  (O).

1. Chứng minh : AO vuông góc BC tại D.
2. Chứng minh : AB2 = AE.AF
3. Chứng minh : tứ giác ODEF nội tiếp.
4. Gọi I, V là trung điểm của AB, AC. tiếp tuyến của (O) tại E và trung trực của AE cắt nhau tại H. chứng minh : H I, V thẳng hàng.