Home » Toán - Math » Các công thức diện tích thường dùng

23/11/13

Các công thức diện tích thường dùng

04:53

Nguyễn Phương


Hình	Công thức	Biến số	Cách đọc
Hình chữ nhật	$a \cdot b \,$	$a$ : Chiều dài, $b$ : Chiều rộng.	Diện tích bằng tích chiều dài 2 cạnh.
Hình vuông	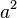$a^2$	$a$ : Chiều dài cạnh hình vuông.	Diện tích bằng bình phương chiều dài 1 cạnh.
Hình bình hành	$a \cdot h$	$a$ : Chiều dài 1 cạnh, $h$ : chiều cao tương ứng với a.	Diện tích bằng 1 cạnh nhân với chiều cao tương ứng với cạnh đó.
Hình thoi	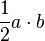$\frac{1}{2}a \cdot b \,$	$a,b$ : Chiều dài 2 đường chéo.	Diện tích bằng 1 nửa tích độ dài 2 đường chéo.
Tam giác	$\frac{1}{2}b \cdot h \,$	$b$ : cạnh đáy, $h$ : chiều cao.	Diện tích bằng 1 nửa tích chiều dài 1 cạnh với đường cao tương ứng với nó.
Hình tròn	$\pi \cdot R^2 \,$	$R$ : bán kính.	Diện tích bằng số pi nhân với bình phương bán kính
Hình e-líp	$\pi \cdot a \cdot b \,$	$a$ và $b$ độ dài nửa trục thực và nửa trục ảo.
Mặt cầu	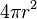$4 \pi r^2 \,$ , hoặc $\pi d^2 \,$	$r$ : bán kính, $d$ : đường kính hình cầu.	Diện tích bằng số Pi nhân với bình phương chiều dài đường kính.
Hình thang	$\frac{1}{2}(a+b)h \,$	$a$ và $b$ : các cạnh đáy, $h$ : chiều cao.	Diện tích bằng trung bình cộng 2 đáy nhân với chiều cao.
Mặt trụ tròn	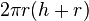$2 \pi r (h + r) \,$	$r$ : bán kính, $h$ : chiều cao.
Diện tích xung quanh của hình trụ	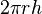$2 \pi r h \,$	$r$ : bán kính, $h$ : chiều cao
Mặt nón	$\pi r (l + r) \,$	$r$ : bán kính, $l$ độ dài đường sinh (slant height).
Diện tích xung quanh của hình nón	$\pi r l \,$	$r$ : bán kính, $l$ độ dài đường sinh (slant height).
Hình quạt	$\frac{1}{2} r^2 \theta \,$	$r$ : bán kính, $\theta$ số đo góc đo bằngradian.

0 Nhận xét :

Đăng nhận xét

Đăng ký: Đăng Nhận xét ( Atom )